State Machines and Dynamic systems

• A simple state machine and several properties
  • Code
• Making the family model dynamic
• Linear Temporal Logic
• Acknowledgments

A simple state machine and several properties

A state machine is a directed graph that models how a system moves from State to State as it executes. It has one or more marked Initial (or starting) states, and edges connecting each state to its successor(s). An initial state can be the successor of another state. Let’s write the following predicates that describe different properties of state machines:

• there is at least one initial state

• a deterministic machine, in which there is one initial state and each state has at most one successor

• a nondeterministic machine, in which there are multiple initial states, or where at least one state has more than one successor, or both

• a machine with at least one state that is unreachable from any initial state

• a machine where all states are reachable from some initial state (it need not be the same initial state for each one)

• a connected machine in which every state is reachable (along the successor relation) from every other state

• a machine with a deadlock: a machine with a state that is reachable from an initial state, but has no successors. For example,

  

  shows a state machine with State0 deadlocked.

• a machine with a livelock: a machine where there exists some cycle reachable from an initial state and a state (the “livelocked” state) reachable from the cycle that’s not part of the cycle. Note that this livelocked state cannot be reached at any point before reaching the cycle or in the cycle itself. For example,

  

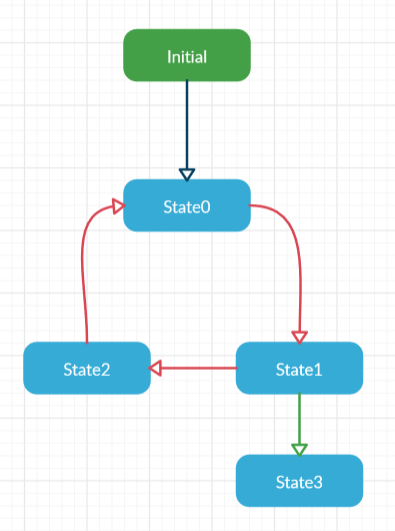
  shows a state machine with State3 livelocked by the cycle starting in State0.

Code

• Alloy anaylizer version:
  • state_machine.als

Making the family model dynamic

We can make the family model dynamic by associating relation with states. Let’s cosider a subset of the family model:

abstract sig Person {
  spouse: lone Person,
}
sig Man, Woman extends Person {}

If we were to make the spouse relation to also consider states, we could simulate that in one state people are married and another they are not. So the above model would include State and have a different spouse relation:

sig State {
    successor : set State
}
abstract sig Person {
  spouse: Person lone -> State,
}
sig Man, Woman extends Person {}

Now whether people are married is dependent on states: in state s people p and q are married if (p+q).spouse.s is non-empty. With this condition we can define an operation that simulates a transition, i.e., a change of states from “these people are not married” to “these people are married”:

pred getMarried [p,q: Person, s1,s2: State] {
  -- Pre-condition: they must not be married
  no (p+q).spouse.s1
  -- Post-condition: After marriage they are each other's spouses
  q in p.spouse.s2
  p in q.spouse.s2
}

With the run command

run {some p,q : Person | some s1,s2 : State | getMarried[p,q,s1,s2] }

we can generate instances where between differente states people get married. The whole code can be found here.

Linear Temporal Logic

The above strategy (plus many other elements) used to be the only way in which dynamic systems (where we reason about transition systems) could be represented in Alloy. However, since Alloy 6 native support has been added to Linear Temporal Logic (LTL), the most commonly used reasoning basis for dynamic systems. Using its temporal operators we could replicate the behavior above with

abstract sig Person {
  var spouse : Person
}

sig Man, Woman extends Person {}

pred getMarried [p, q : Person]
{
  not p in q.spouse
  not q in p.spouse
  after p in q.spouse
  after q in p.spouse
}

run {some p,q : Person | getMarried[p,q]}

Note that in the vizualization of the instance in the Alloy Analyzer is different, as it directly shows the different states of the system. The spouse relation changes between states because it’s marked with the var keyword. The predicate after forces something to be true in the next state. So to get married, two people that are not married to each other become married in the following steps.

We study these operators and how to specify dynamic systems with them.

Acknowledgments

Thanks to Tim Nelson for sharing examples about the state machine model. Thanks to Cesare Tinelli for the family model material, itself based on the original Alloy model by Daniel Jackson distributed with the Alloy Analyzer.